Exemples de cryptologie
Exemples de cryptologie
Étant donné que le chiffrement symétrique est tellement plus rapide, vous pouvez d’abord générer une clé secrète et la transmettre sur une ligne sécurisée par la cryptographie de la clé publique. Maintenant, toute communication future peut utiliser la clé secrète.
Différence entre la cryptographie et la cryptologie
Cryptographie L’étude de la conversion du texte brut (format lisible) est-il en texte chiffré (format non lisible) i.e. chiffrement. Il est également appelé le étude du cryptage. Cryptologie, D’un autre côté, est l’étude de la conversion du texte brut en chiffre d’affaires et vice versa. Il est également appelé le Étude du chiffrement et du décryptage.  Une différence majeure est que la cryptologie est le parent de la cryptographie.
Une différence majeure est que la cryptologie est le parent de la cryptographie.  Voyons les autres différences.
Voyons les autres différences.
| SL Non. | Cryptographie | Cryptologie |
|---|---|---|
| 1. | La cryptographie est le processus de conversion du texte brut en texte chiffré. | La cryptologie est le processus de conversion du texte brut en texte chiffré et vice versa. |
| 2. | Il est également appelé l’étude du cryptage | Il est également appelé l’étude du chiffrement et du décryptage. |
| 3. | Il se déroule du côté de l’expéditeur | Il a lieu du côté expéditeur et récepteur |
| 4. | En cryptographie, l’expéditeur envoie le message au récepteur. | En cryptologie, l’expéditeur et le récepteur s’envoient des messages. |
| 5. | La cryptographie peut être considérée comme l’enfant de la cryptologie. | La cryptologie peut être considérée comme le parent de la cryptographie |
| 6. | La cryptographie traite des techniques de communication sécurisée. | La cryptologie traite de l’étude de la communication sécurisée. |
| 7. | La cryptographie se concentre sur la pratique de la cachette d’informations | La cryptologie se concentre sur les aspects théoriques et mathématiques de la sécurité de l’information |
| 8. | La cryptographie implique des techniques de chiffrement, de décryptage et d’authentification | La cryptologie implique l’étude des codes, des chiffres et de la cryptanalyse |
| 9. | La cryptographie concerne le développement d’algorithmes et de protocoles | La cryptologie concerne l’analyse et la rupture des méthodes de chiffrement existantes |
| dix. | Cryptographie utilisée dans divers domaines tels que la finance, le commerce électronique et la sécurité nationale | Cryptologie utilisée dans le monde universitaire et la recherche pour comprendre et améliorer le chiffrement |
| 11. | La cryptographie comprend des applications telles que la messagerie sécurisée, le transfert de fichiers sécurisé et les signatures numériques. | La cryptologie comprend des applications telles que la cryptanalyse, la rupture de code et l’analyse mathématique des méthodes de chiffrement. |
Dernière mise à jour: 09 mars 2023

Comme un article
Cryptologie
Ces notes servent d’introduction à la crypto et non à un programme complet pour faire de vous un expert qui est autorisé à mettre en œuvre des chiffres, des hachages, des signatures ou de ce type dans une application réelle. Bien sûr, c’est bien de jouer à la maison, mais n’essayez jamais de mettre en œuvre des routines cryptographiques pour un client ou votre propre entreprise. Laissez-le aux pros. Il y a de bonnes bibliothèques là-bas. Utilise les.
Cependant, vous devez toujours vérifier et demander si la bibliothèque que vous utilisez implémente un algorithme qui n’a pas encore été fissuré et a une longueur de clé suffisante.
Cela a été une annonce de service public importante.
Arrière-plan
Il est conventionnel de parler de Crypto dans un cadre avec quelques personnages nommés Alice (l’expéditeur), Bob (le récepteur), Eve (The Eyesdropper) et Mallroy (un puissant acteur malveillant).
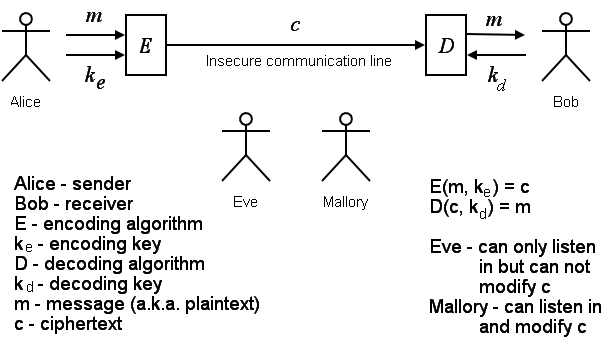
Alice et Bob peuvent être des personnes, des clients et des serveurs, des ordinateurs de pairs, des magasins de données, des routeurs de réseau, etc. Eve peut observer la communication. Mallory peut non seulement écouter mais aussi usurper l’un des participants, ajouter, modifier ou supprimer des messages réels, détourner la connexion, faire un déni de service, injecter des logiciels malveillants, etc.
Objectifs:
- : Il devrait coûter plus cher à récupérer $ M $ que M $.
- : Bob devrait être en mesure de vérifier que c’est Alice qui a envoyé $ M $.
- : Bob devrait être en mesure de vérifier que $ m $ n’était pas falsifié.
- : Alice ne devrait pas pouvoir nier d’envoyer $ m $.
- Si votre algorithme secret est compromis (quelqu’un pourrait quitter votre groupe), vous devez le changer, et c’est beaucoup plus difficile que de simplement changer une clé!
- Les algorithmes publics peuvent être soumis à des milliers d’experts à la recherche de défauts, vous avez donc un certain degré de confiance dans ceux qui résistent à un examen minutieux.
Définitions
Paroles à savoir: Cryptographie L’art et la science de fabrication chiffres. Cryptanalyse l’art et la science de rupture Ciphers, je.e., L’extraction de $ m $ étant donné $ c $, $ e $, $ d $ et éventuellement $ k_e $. Cryptologie L’étude de la cryptographie et de la cryptanalyse.
Exercice: Découvrez la stéganographie. En quoi est-ce différent de la cryptographie?
Cryptosystème Une suite particulière d’algorithmes et de protocoles pour le cryptage, le décryptage et la génération de clés. Exemples: cryptosystème Cramer-Shoup, Rabin Cryptosystème, cryptosystème Benaloh, cryptosystème RSA. Système cryptographique Tout système qui utilise la cryptographie. Cipher Un algorithme utilisé dans un cryptosystème.
Exercice: En quoi un «code» est-il différent d’un «chiffre»? Les codes sont-ils plus sécurisés que les chiffres? Pourquoi ne sont-ils pas utilisés aussi souvent?
Confusion la propriété d’avoir la relation entre le texte en clair, le texte chiffré et la clé si compliquée qu’elle est inutile pour le cryptanalyste. Diffusion La propriété d’avoir des modèles statistiques dans le texte en clair se propage largement à travers le texte chiffré.
Délais
- L’article de l’histoire de la cryptographie de Wikipedia
- Wikipedia de Wikipedia
- La chronologie de Carl Ellison
Types de chiffres
- : Un chiffre assez facile pour être effectué à la main, généralement basé sur des caractères. Aussi appelé .
- : À peu près n’importe quel chiffre qui n’est pas classique.
- : Chaque caractère du texte en clair est remplacé par un ou plusieurs caractères pour faire le texte chiffré.
- : Les caractères dans le texte en clair sont réorganisés pour former le texte chiffré.
- : Un chiffre de substitution dans lequel un caractère du texte en clair est toujours remplacé par le même caractère.
- : Un chiffre de substitution qui utilise essentiellement plusieurs mappages de substitution monoalphabétiques.
- : Une substitution dans laquelle un personnage peut mapper à l’un des caractères.
- : Une substitution de blocs de caractères pour des blocs de caractères.
- : Un chiffre polyalphabétique dans lequel le schéma de remplacement se répète.
- : Explicite si vous comprenez périodique.
- : Le cryptage se déroule non pas par caractère mais par blocs de caractères.
- : Un chiffre fonctionnant sur un flux de données de longueur inconnue, incorporant généralement des commentaires.
- : Un chiffre dans lequel $ k_e $ et $ k_d $ sont identiques ou trivialement les uns des autres; nécessite que les parties se réunissent en secret pour échanger les clés qu’ils utiliseront. Aussi appelé .
- : Un schéma dans lequel la clé de cryptage de chacun est connue publiquement, mais sa clé de décryptage est gardée secrète. Aussi appelé .
Les chiffres sont amusants à étudier, mais ils varient considérablement en termes d’utilité de la sécurité. L’un des plus grands défauts de sécurité d’un système est de mal utiliser la crypto. C’est vrai: le problème est son abus, pas son omission!
Ce n’est pas parce qu’un chiffre est répertorié sur cette page que vous devez l’utiliser. Notre objectif est d’apprendre un large éventail de chiffres, à la fois historiques et modernes.
Cryptographie clé secrète
- Si $ n $ dans un groupe doit communiquer, ils ont besoin de clés $ \ frac $.
- Les clés doivent être distribuées en toute sécurité (en secret).
- Les clés doivent être maintenues en sécurité.
- Les clés doivent être changées fréquemment, qui renvoient dans le mal de tête de distribution.
Dans les exemples basés sur des caractères ci-dessous, nous supposerons (sans aucune perte de généralité) un alphabet symbole de 26 (un..Z).
Caesar Cipher
Un chiffre complètement pathétique et peu sûr par les normes modernes. La clé de chiffrement $ k_e $ est un petit entier et $ k_d = k_e $. Pour crypter, ajoutez $ k_e $ à chaque caractère en clair; pour décrypter, soustraire. Par exemple, avec k = 5, AttackAtDawn devient fyyfhpfyifbs trivial to craque: Devinez $ k_e $.
Substitution monoalphabétique
Au lieu d’ajouter simplement un décalage fixe à chaque personnage, vous pouvez précomputer un table de substitution en générant une permutation aléatoire de votre alphabet. Par exemple:
ABCDEFGHIJKLMNOPQRSUVWXYZ MQHPSVJYCURFTBILAKWNGZDOEX
Donc AttackAddawn est maintenant mnnmhrmnpmdb . Vous ne craquez pas cela en devinant la clé (il y a $ n!$ touches possibles), mais l’analyse de fréquence peut casser n’importe quel chiffre de substitution monoalphabétique, à condition que le message soit suffisamment long. Pour les techniques dont la clé est une permutation, une façon de rendre la clé plus facile à retenir est de choisir une phrase, de disposer ses lettres uniques, puis de remplir les lettres manquantes dans l’ordre. Par exemple, l’optimisation prématurée est la racine de tout le mal donne cette cartographie de substitution:
Prematuoiznshflvbcdgjkqwxy
Substitution homophonique
Chaque lettre en clair par rapport à un ou plusieurs symboles dans le texte chiffré. Le nombre de cibles doit être proportionnel à sa fréquence (pour vaincre l’analyse de fréquence). Exemple:
A 12 15 36 50 56 70 81 95 B 51 84 C 16 44 65 D 04 06 48 82 E 01 17 19 34 47 49 58 60 67 77 85 90 F 13 27 G 09 28 H 26 42 53 59 68 71 I 35 73 76 86 91 96 J 18 K 07 L 29 40 54 87 M 25 30 N 21 61 62 69 74 94 O 02 03 08 10 57 75 93 P 41 98 Q 97 R 32 38 43 45 80 83 S 14 22 39 79 89 99 T 00 20 23 33 46 52 72 78 88 U 11 64 66 V 37 W 63 92 x 31 y 24 55 Z 05
Pour crypter, choisir au hasard parmi les possibilités. Par exemple, un cryptage possible de AttackAtdawn est:
56 78 20 95 65 07 12 72 06 50 92 61
Vigène simple
Le chiffre connu sous le nom de Vigenère n’a pas été inventé du tout. Il semble avoir été décrit pour la première fois par Giovan Battista Bellaso. La clé est une chaîne que vous ajoutez au texte en clair avec l’ajout modulaire, comme dans cet exemple (a = 0, b = 1, c = 2, . Z = 25):
Texte en clair: TakeacopyofyourpolicyTonorawilcoxontheThirdfloor Key: Quarkquarkquarkquarkquarkquarkquarkquarkquarkquar corpertex
Pour générer un texte chiffré à la main, vous pouvez utiliser une roue de code ou une tabula recta. Ce schéma n’est pas sécurisé car la clé se répète. Si la longueur de clé peut être déterminée, le cryptanalyste peut effectuer plusieurs analyses de fréquence (une pour chaque valeur de décalage dans la clé). Les méthodes de détermination de la longueur de clé sont la méthode de Kaisiski et le test Friedman. Pour les données binaires (i.e., Une séquence de bits) Modular Addition Base-2 n’est qu’un simple XOR. Exemple:
PlainText: 011000010101000011110100101010101001000000111111111 Clé: 0000011100000111000001110000011100000111000001110 INCHERTTEXT: 0110011001011111100111111111111110110011
Vigène de clé automatique
Vigenère a en fait créé un chiffre autokey qui est plus fort car la clé ne répète jamais. Au lieu de cela, la «clé» est composée du phrase de clé suivi du texte en clair, comme ceci:
PlainText: TakeacopyofyourpolicyTonorawilcoxontheThirdfloor Key: QuarkTakeAcopyofyourpolicyTorAwilCoxontheThird CirherText: Jukvkvozcohmdsfumzctnhzvqpfojwcootwyvvbhyhyswfu
Celui-là a utilisé le texte en clair dans le cadre de la clé. Vous pouvez également utiliser le texte chiffré. Regarde comment?
Ciphers de la clé automatique moderne
Vous pouvez toujours casser les chiffres Autokey Vigenère par analyse linguistique, car la clé contient du texte et est donc susceptible d’avoir des lettres à haute fréquence. Les chiffres modernes des touches automatique génèrent les valeurs de décalage avec un générateur de nombres aléatoires. Les graines clés du générateur.
Exercice: Implémentez un chiffre Autokey dans le langage de programmation de votre choix.
Pavé à un temps
- est aussi long ou long que le message crypté
- est vraiment généré au hasard
- est utilisé une fois et une seule fois
Exercice: Pourquoi les coussinets sont-ils couramment utilisés, étant donné qu’ils sont les chiffres les plus sécurisés possibles?
Jouer franc jeu
Ceci est un exemple de . Il remplace les paires de personnages. La clé est une permutation de
Z c b m l g d a q e t u o k h f s x v n p i y r w
- Soit $ (a, b) $ la ligne et la colonne du premier caractère et $ (c, d) $ être la ligne et la colonne du second.
- Si $ a \ neq c $ et $ b \ neq d $, retournez $ (a, d) (b, c) $.
- Si $ a = c $, retournez $ (a, (b + 1) \ bmod 5) (c, (d + 1) \ bmod 5) $.
- Si $ b = d $, retournez $ ((a + 1) \ bmod 5, b) ((c + 1) \ bmod 5, d) $.
Puis attaque de l'est ⇒ th en à xt ac kf ro mt he xe comme tx ⇒ ut hw go fo db tv yk zk nh na dx de ⇒ uthwgofodbtvykzknhnadxof
Le décryptage exécute les règles à l’envers. Le chiffre de playfair est assez peu sûr.
Carré
Crypte les digraphs comme Playfair, mais légèrement plus forts car il permet des lettres doubles et ne donne pas de digraphes en texte chiffré inversé pour les digraphes en texte en clair inversé. Exemple
A B C D E G I V E M F G H I K L B R T Y L M N O P O D A H C Q R S T U F K N P Q V W X Y Z S U W X Z P R E M A A B C D E T U O I Z F G H I K N S H F L L L O P V B C D G Q R S T U K Q W X V W X Y
Puis attaque de l'est ⇒ th en ta ck from the tx ⇒ ni vl ev fm mo bv df ni ma vv nx ⇒ uthwgofodbtvykzknhndxof
D’accord, si légèrement plus fort que Playfair mais alors quoi? Les ordinateurs peuvent casser ces choses en quelques secondes, ou peut-être des minutes (avec suffisamment de texte chiffré).
Transposition de blocs simple
Le chiffre de transposition le plus simple divise le message en blocs de taille $ n $, puis brouille chaque bloc selon une permutation de $ (1..n) $. Par exemple, si notre clé est (4,1,6,3,2,5) $, le message GetThathealthInspector est crypté comme tgatehattehlsheniprcot .
Transposition colonne
Écrivez la ligne de message par ligne dans une grille, puis lisez-la dans des colonnes. Totalement insécurité. La clé est juste le nombre de lignes. Devine ça.
Clôture
La clôture ferroviaire n’est pas meilleure que la précédente, juste plus funk. La clé est le nombre de rails sur lesquels vous écrivez le texte en clair de haut en bas, générant le texte chiffré en lisant un rail à la fois. Exemple: pour crypter “remplir et déposer un formulaire WS2475” sur 4 rails:
f t l 4 m i u a i e 2 7 r l o n f a s 5 o l d w f
Vous lisez ensuite le texte chiffré “ftl4miuaie27rlonfas5oldwf” . C’est trivial pour se fissurer. Devinez simplement $ k $.
Combiner la substitution et la transposition
La transposition seule est très faible; La substitution seule est très faible; Les combiner est mieux. Vous pouvez mélanger une grande partie des chiffres de substitution classiques avec diverses transpositions, ou utiliser des chiffres de combinaison spéciaux comme le bifid. De plus, la plupart des célèbres machines de rotor et des chiffres modernes utilisent cette combinaison; en fait ils appliquent ces transformations plusieurs fois.
Bifide
Celui-ci remplace les lettres par leurs coordonnées dans une grille et effectue une transposition en colonnes sur les coordonnées. Exemple:
Z c b m l g d a q e t u o k h f s x v n p i y r w
Écrivez les coordonnées (colonne, colonne) sous chaque lettre du texte en clair (E.g., “A” est à la ligne 1, colonne 2; “T” est à la ligne 2, colonne 0, etc.):
Attackatdawn 122102121143 200213201244
Ensuite, lisez en rangées, groupe par deux et recherchez les lettres de texte chiffré:
122102121143200213201244 A U B A D R T B Q T A W
Trifide
Comme bifid, mais sur un cube. Exemple:
Z C B M L F V N P G D A Q E X I R W T U O K H S Y . J
Pour crypter, écrivez d’abord les coordonnées:
AttackatDawn 000001000022 122102121110 200210201221
000001000022122102121110200210201221 Z C Z O S F H Q V I N .
Énigme
- Aucune lettre ne crypterait à lui-même
- L’auto-régime signifiait qu’il y avait moins de possibilités de configuration de brouillage
- C’était vraiment facile de trouver des berceaux. La plupart des messages ont commencé par un rapport météo.
- Au début, les clés de message sont apparues deux fois successivement.
Méthodes cryptographiques modernes
- Opérez sur des chaînes de bits, pas des chaînes de caractère
- Font attention à masquer complètement les motifs et les redondances dans le texte en clair
- Utiliser aléatoire Clés (qui peuvent également être réutilisées)
- Assurez-vous que de très légères changements dans le texte en clair affectent une grande partie du texte chiffré (et vice versa). C’est ce qu’on appelle le Effet d’avalanche.
- Efficace
- Tolérance de panne
- BCE – livre de codes électronique
- CBC – chaînage de blocs de chiffre
- CFB – Retour de chiffre
- OFB – Retour de sortie
- Ctr – compteur
- BC – chaînage de blocs
- PCBC – Propagation de chaînage de blocs de chiffre
- CBCC – Chaîne de bloc de chiffre
Des
IDÉE
RC4
Rc6
Flowfish
Deux Poisson
Stimulation
Chez Wikipedia AES est la nouvelle norme, remplaçant DES. C’était le gagnant du concours (en 2001), où est soumis sous le nom de Rijndael, battant RC6, Serpent, Mars et Twofish.
Échange de clés

Diffie et Hellman (les lauréats du prix Turing 2015) et leur ami Merkle ont montré en 1976 qu’il était possible pour deux personnes d’échanger une clé secrète sans avoir à se rencontrer en secret:
- Alice choisit un Prime $ N $ et envoie ceci dans le clair à Bob
- Alice choisit une racine primitive mod $ n $ (comment trouver), appelé $ g $, et envoie ceci dans le clair à Bob
- Alice choisit un entier secret $ a $ et envoie $ g ^ a \ bmod n $ en clair à Bob
- Bob choisit un entier secret $ b $, et envoie $ g ^ b \ bmod n $ en clair à Alice
- Alice calcul ($ g ^ b \ bmod n) ^ a \ bmod n $ et bob calcul ($ g ^ a \ bmod n) ^ b \ bmod n $. C’est la clé! (C’est $ g ^ \ bmod n $)
Ceci est probablement sécurisé, à condition que $ n $ soit très important et $ \ frac $ est également prim $, il y a Aucun moyen efficace connu Pour obtenir $ a $ ou $ b $ parmi ces. C’est le problème du logarithme discret, rappelez-vous? Exemple avec petit $ n $:
- Alice choisit $ n = 208799 $ et $ g = 13 $ et les envoie à Bob
- Alice choisit $ a = 152335 $ et Bob choisit $ b = 98113 $
- Alice envoie Bob 13 $ ^ \ bmod 208799 = 73033 $
- Bob envoie Alice 13 $ ^ \ bmod 208799 = 147540 $
- Alice calcule 147540 $ ^ \ BMOD 208799 = 8435 $
- Bob calcule 73033 $ ^ \ bmod 208799 = 8435 $
- La clé secrète est de 8435 $.
Ne faites pas cela avec de petites valeurs de $ n $. En général, à moins que vous n’obteniez une sorte de certification, n’essayez pas de sécuriser les systèmes du monde réel. Mais bien sûr, allez-y et apprenez les algorithmes et pratiquez le codage pour l’instant.
Cryptographie par clé publique
Les chiffres de clés publics résolvent le cauchemar de gestion clé des chiffres clés secrètes, au prix de la vitesse. Dans un groupe de personnes N $, on n’a besoin que de clés publiques $ n $ et de clés privées $ n $.
Cryptosystème RSA
- Génère deux grands nombres premiers, $ p $ et $ q $.
- Choisit une valeur $ e $ relativement prime pour $ (p-1) (q-1) $.
- Publie sa clé publique $ (n, e) $ où $ n = pq $.
- Calcule $ d $ = inverse modulaire de $ e $ par rapport à $ (p-1) (q-1) $, en gardant secret.
- Détruit $ p $ et $ q $.
- Pour qu’Alice envoie un message $ m $ à Bob, elle envoie $ c = m ^ e \ bmod n $.
- Bob décrypte cela facilement parce que $ m = c ^ d \ bmod n $.
Exercice: Recherchez les mathématiques derrière RSA. Pourquoi ça marche, en détail? Votre réponse utilisera les théorèmes sous-jacents à la fonction totale d’Euler; Assurez-vous de montrer comment il réduit à $ (P-1) (Q-1) $ lorsque $ pq $ est primordial, entre autres choses.
Exercice: Diffie-Hellman (DH) est parfois considéré comme faisant partie de la cryptographie de clé publique, même s’il traite de l’échange de clés et n’est pas lui-même un algorithme de chiffrement. Pourquoi, alors, certaines personnes considèrent-elles la clé publique? (La réponse à cela nécessite des recherches.)
Pour un exemple trivial, juste pour que vous puissiez voir les mathématiques en action, faisons un RSA avec des clés 32 bits:
Cet exemple est pour l’illustration uniquement. N’implémentez jamais votre propre algorithme de crypto. Assurez-vous également de comprendre à quel point la cryptographie par clés publique est horrible avec de si petites clés. Les vraies clés devraient avoir des milliers de bits.
Nous générons d’abord deux nombres premiers 16 bits aléatoires (16 parce que c’est la moitié de la taille des clés, qui est 32): $ \ begin
C2 BF 44 C3 B3 6E 64 65 20 65 73 74 C3 A1 20 75 64 2E 3F
Nous voulons diviser notre message en blocs. La taille du bloc recommandée est $ \ lfloor \ frac \ rfloor $. Puisque nous faisons RSA-32 (touches 32 bits), nous voulons $ \ lfloor \ frac \ rfloor $, ou 3. Alors, regroupons nos octets en blocs de trois:
C2BF44 C3B36E 646520 657374 C3A120 75642E 3F0202
Le 02 02 à la fin est le rembourrage PKCS # 7 pour faire du message un multiple de 3 octets. En décimal, nos blocs sont 12762948, 12825454, 6579488, 6648692, 12820768, 7693358, 4129282. Appliquons maintenant la fonction de crypte à chacun :: 12762948 ^ \ bmod 1857329701 = 1674934738 $
12825454 $ ^ \ BMOD 1857329701 = 920121142 $
6579488 ^ \ BMOD 1857329701 = 703310795 $
6648692 ^ \ BMOD 1857329701 = 1740932196 $
12820768 ^ \ BMOD 1857329701 = 512101030 $
7693358 $ ^ \ BMOD 1857329701 = 1327283085 $
4129282 ^ \ BMOD 1857329701 = 1468977038 $
That’s the ciphertext in decimal, namely 1674934738, 920121142, 703310795, 1740932196, 512101030, 1327283085, 1468977038 To decrypt: $1674934738^ \bmod 1857329701 = 12762948$
920121142 ^ \ BMOD 1857329701 = 12825454 $
703310795 ^ \ BMOD 1857329701 = 6579488 $
1740932196 ^ \ BMOD 1857329701 = 6648692 $
512101030 ^ \ BMOD 1857329701 = 12820768 $
1327283085 ^ \ BMOD 1857329701 = 7693358 $
1468977038 ^ \ BMOD 1857329701 = 4129282 $
Nous remettons le message d’origine! Pour le plaisir, voyez comment l’exemple ci-dessus a été généré.
Étant donné que le chiffrement symétrique est tellement plus rapide, vous pouvez d’abord générer une clé secrète et la transmettre sur une ligne sécurisée par la cryptographie de la clé publique. Maintenant, toute communication future peut utiliser la clé secrète.
Exercice: Pourquoi serait-il faux d’utiliser une taille de bloc de 4 octets dans l’exemple ci-dessus?
Hachage cryptographique
- Trouver un message qui hache à une valeur donnée ()
- Trouvez deux messages qui hachent à la même valeur ()
Mathématiquement, une fonction de hachage cryptographique $ h $ produit un hachage à partir d’un message, $ h (m) = c $, de sorte que $ m $ ne peut pas être déterminé efficacement à partir de $ c $, et on ne peut pas trouver efficacement $ m_1 \ neq m_2 $ tel que $ h (m_1) = h (m_2) $,
Habituellement, le changement d’un seul bit dans le message entraînera un apparence complètement et totalement différente.
$ Cat Will C'est ma volonté. Je laisse 1000 dollars à Alice et tout le reste à Bob. Signé, Eve. $ md5sum C18FEB890752C9E680C99D1E909FD761 Will $ sed "s / 1/9 / g" $ Cat Will C'est ma volonté. Je laisse 9000 dollars à Alice et tout le reste à Bob. Signé, Eve. $ md5sum 85570BC2D0458B1F98F484261DEE7D4D
Un hachage sécurisé fournit un moyen de déterminer si un message a été falsifié. Voir Guide illustré de Steve Friedl sur les hachages cryptpgraphiques.
Codes d’authentification des messages
Ceux-ci sont similaires aux hachages cryptographiques, sauf qu’ils utilisent une clé secrète, tandis que les hachages utilisent simplement le message lui-même. $ \ matt
- Macs vs. Hachages à Stackoverflow
- Signatures numériques à Wikpedia
- Mac à Wikipedia
Signatures numériques
Comment Bob peut-il être sûr que le message est venu d’Alice et pas de quelqu’un d’autre? Par Alice signature il; c’est comme ça. En pratique, on signe généralement un hachage, pas le message entier .
RSA pour les signatures numériques
Pour qu’Alice envoie un message à Bob,
- Alice crypte M avec sa clé privée
- Alice crypte avec la clé publique de Bob
- Bob décrypte avec sa clé privée
- Bob décrypte avec la clé publique d’Alice
DSA
Cryptanalyse
- Analyse de fréquence
- Attaque en texte en clair connu
- Attaque connue du texte chiffré
- Attaque en texte en clair choisi
- Attaque clé choisie
- Cryptanalyse linéaire
- Cryptanalyse différentielle
- Vol
- Corruption
- Chantage
Exercice: Faites de l’auto-apprentissage sur la cryptanalyse ou trouvez un cours en ligne amusant.
Exemples de programmation
Heh, nous n’allons pas montrer comment rouler votre crypto. Nous allons regarder des bibliothèques exsitantes réelles.
Transmettez-vous des données sur un réseau IP?
Pour les autres parties de votre application nécessitant un chiffrement, lisez la suite.
Exemples JavaScript
Module intégré: Node crypto .
Exemples Python
Exemples Java
Référence: Java Cryptography Architecture (JCA)
Meilleures pratiques de sécurité pour Crytpo
- Jamais jamais jamais rouler le vôtre
- Utilisez une bibliothèque bien testée qui est à jour, examinée par des experts et jugée en sécurité pour l’instant
- N’utilisez pas un algorithme qui a été fissuré
- N’utilisez pas un algorithme qui peut théoriquement être fissuré
- N’utilisez pas un algorithme qui a un défaut exploitable
- Utilisez le bon type d’algorithme pour vos besoins, E.g., Le hachage du mot de passe doit être lent, alors utilisez quelque chose comme Bcrypt.
- Utilisez des tailles de clés qui sont assez longues
- Si vous stockez le mot de passe hachis, utilisez toujours du sel
- Utilise des vecteurs d’initialisation et des nonces plutôt que de les ignorer
- Soyez humble: vous n’êtes probablement pas un expert dans ce
Résumé
- Contexte et définitions
- Types de chiffres
- Différence entre la clé secrète et la cryptographie de la clé publique
- Échange de clés
- Hachage et signatures numériques
- Cyrptanalyse
- Exemples de programmation
